Suki Tekverk, a summer intern, spent the last two weeks here studying APL. She will be a high school senior next September and is adept in math, so in addition to APL we also considered some math problems, proofs, and proof techniques, including the following:

Given line segments x and y, construct (using compass and straight-edge) line segments for the following values:
   x+y
   x-y
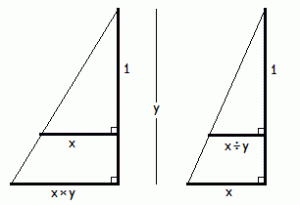
   x×y
   x÷y

The first two are immediate. Constructing the last two are straightforward if you are also given 1 (or some other reference length from which to construct 1). Can you construct x×y and x÷y without 1?

Constructing x÷y is impossible if you are not given 1 : From x and y alone you can not determine how they compare to 1. If you can construct x÷y, then you can construct x÷x and therefore relate x and y to 1, contradicting the previous statement.

Can you construct x×y without 1? I got stuck (and lazy) and posed the question to the J Chat Forum, and received a solution from Raul Miller in less than half an hour. Miller’s proof recast in terms similar to that for x÷y is as follows:

From x and y alone you can not determine how they compare to 1. If you can construct x×y, then you can construct x×x, whence:
   if x<x×x then x>1
   if x=x×x then x=1
   if x>x×x then x<1
contradicting the previous statement.

I last thought about this problem in my first year of college many decades ago. At the time Norman M. (a classmate) argued that there must be a 1 and then did the construction for x÷y using 1. I recall he said “there must be a 1” in the sense of “1 has to exist if x and y exist” rather than that “you have to use a 1 in the construction” or “you can not construct x÷y without using 1”. I don’t remember what we did with x×y; before Miller’s message I had some doubt that perhaps we were able to construct x×y without using 1 all those years ago. (Norman went on to get a Ph.D. at MIT and other great things.)

Follow

by Suki Tekverk

As a born and raised New Yorker, I thought I had seen it all, but two short weeks spent in Vancouver with Roger Hui and his family proved me very wrong! I went from being at the top of the totem pole to one of the most clueless people around. Luckily, these new experiences provoked new paths of thought and ultimately left me more prepared to face the world than I was when my plane shakily landed in this foreign place.

Upon my arrival, I was greeted by Stella, Roger’s wife, and their children, Nicholas and Rachel, who promptly made me a sign for my bedroom door, making me feel right at home.

The next morning, I went right to work, unsuccessfully writing a dfn for the Fibonacci sequence. After struggling for at least 40 minutes, Roger showed me a solution. This solution was nearly the exact definition of the Fibonacci sequence, setting a precedent for the uncomplicated and direct solutions that ensued. Over the next week we ripped through a Monty Hall simulation, recursive Peano addition and multiplication, recursive and non-recursive binomial coefficients, the Cantor set, the Sierpinski Carpet and more. Over this week, I not only discovered new realms of mathematics but also ate foreign food, hiked through a canyon, watched a Chinese film, made cookies, went to a horse ranch, listened to an orchestra performance, experienced sugar withdrawal and saw a sunset on a mountain. This was just the first week.

The main focus of week two was proofs. At first, I was skeptical of the value of writing proofs in APL as opposed to writing them on paper, but being able to run each step of the proof was quite useful. I started with proof by induction, then by contradiction. After learning the basics I proved the sum of an arithmetic series, sum of geometric series, sum of integers, sum of odd integers and sum of binomial coefficients. This week showed me how closely APL and mathematical notation align. However, I am still annoyed by the fact that the order of operations isn’t how I learnt it in school; it will take some getting used to. My next task will be buying a Windows computer for APL.

Overall, these two weeks in Vancouver were a great learning experience on many levels. Coding in APL has led me to consider possible career options as well as help me understand the nature of the language. Living in a city so far away from home made me question things I considered commonplace and forced me to realize that New York is only a small part of a much larger world.

Follow