As part of the bigger, overarching refactoring goal of making Py’n’APL great again, I refactored some of the code that deals with sending data from Python to APL and receiving data from APL into Python. In this blog post, I will describe – to the best of my abilities – how that part of the code works, how it differs from what was in place, and why those changes were made.
The starting point for this blog post is the commit b7d4749.
This blog post is mostly concerned with the files Array.py, ConversionInterface.py, and ObjectWrapper.py (these were the original file names before I tore them apart and moved things around). It does not make much sense to list where all the things went, but you can use GitHub’s compare feature to compare the starting commit for this blog post with the “final” commit for this blog post.
State of Affairs
If you are going to refactor a working piece of code, the first thing you need to do is to make sure that you know what the code is doing! This will help to ensure that your refactoring does not break the functionality of the code. With that in mind, I started working my way through the code.
I started by looking at the file ConversionInterface.py and the two classes Sendable and Receivable that were defined in there. By reading the comments, I understood that these two classes were defining the “conversion interface”. In this context, the word “interface” has approximately the Java meaning of interface: it defines a set of methods that the classes that inherit from these base classes have to implement. For the class Sendable, there are two methods toJSONDict and toJSONString; and for the class Receivable, there is one method to_python.
Even though I had just started, I already had a couple of questions:
- Do the names
SendableandReceivablemean that these objects will be sent to/received from APL or from Python respectively? - Why is there a comment next to the definition of
Sendablethat says that classes that implement a methodfrom_pythonwill inherit fromSendable? Is that a comment that became a lie as the code evolved? If not, why isn’t there a stub for that method in the class itself?
The more I pondered on these questions, the more I started to think that the “conversion interface” isn’t necessarily about the sending to/receiving from APL, but rather the conversion of built-in Python types to helper classes like APLArray or APLNamespace (from the file Array.py) and back. So, it might be that Sendable and Receivable are supposed to be base classes for these helper classes, telling us which ones can be converted to/from built-in Python types. I needed to solve this conundrum before I could prepare these two base classes and use Python mechanisms to enforce these “interfaces”.
What the Interface Really Means
After playing around with the code a bit more, I felt more confident that Sendable should be inherited by classes that represent things that can be sent to APL and Receivable represents things that can be received from APL. However, it must be noted that Py’n’APL doesn’t send Python built-in types directly to APL. Whenever we want to send something to APL, Py’n’APL first converts it to the suitable intermediate (Python) class. For example, lists and tuples are converted to APLArray, and dictionaries are converted to APLNamespace.
If an APLArray instance is supposed to be sendable to APL, we must first be able to build it from the corresponding Python built-in types, and that is why almost all Sendable subclasses also implement a method from_python. Looking at it from the other end of the connection, Receivable instances come from APL and Py’n’APL starts by taking the JSON and converting it into the appropriate APLArray instances, APLNamespace instances, etc. Only then can we convert those intermediate representations to Python, and that is why all Receivable subclasses come with a method to_python. In addition, those Receivable instances come from APL as JSON, so we need to be able to instantiate them from JSON. That is why Receivable subclasses also implement a method fromJSONString, although that is not defined in the Receivable interface.
So, we have established that APL needs to know how to make sense of Python’s objects and Python needs to know how to make sense of APL’s arrays. (In Python, everything is an object, and in APL, everything is an array. In less precise – but maybe clearer – words, Python needs to be able to handle whatever APL passes to it, and APL needs to be able to handle whatever Python passes to it.) To implement this, we need to determine how Python objects map to APL arrays and how APL arrays map to Python objects. This is not trivial, otherwise I wouldn’t be writing about it! Here are two simple examples showing why this is not trivial:
- Python does not have native support for arrays of arbitrary rank.
- APL does not have a key-value mapping type like Python’s
dict.
To solve the issues around Python and APL not having exactly the same type of data, we create lossless intermediate representations in both host languages. For example, Python needs to have an intermediate representation for APL arrays so that we can preserve rank information in Python. When possible, intermediate representations should know how to convert into the closest value in the host language. For example, the Python intermediate representation of a high-rank APL array should know how to convert itself into a Python list.
I began by looking at the handling of APL arrays and namespaces. These are the conversions that need to be in place:
- APL arrays ←→ Python lists
- APL arrays ← arbitrary Python iterables
- APL namespaces ←→ Python dictionaries
When sending data from the Python side, it first needs to be converted into an instance of the appropriate APLProxy subclass. For example, a dictionary will be converted into an instance of APLNamespace. That object is converted to JSON, which is then sent to APL. APL receives the JSON and looks for a special field __extended_json_type__, which identifies the type of object. In this example, that is "APLNamespace". APL then uses that information to decode the JSON data into the appropriate thing (a namespace in this example).
When sending data from the APL side, a similar thing happens. First, the object is converted into a namespace that ⎕JSON knows how to handle. For example, an array becomes a namespace with attributes shape (the shape of the original array) and data (the ravel of the original array); the namespace is tagged with an attribute __extended_json_type__, which is a simple character vector informing Python what the object is. That namespace gets converted to JSON with ⎕JSON, and the JSON is sent to Python. Python receives the JSON and decodes it into a Python dictionary. Python then uses __extended_json_type__ to determine the actual object that the dictionary represents (an array, in our example) and uses the information available to build an instance of the appropriate APLProxy subclass (APLArray in this example).
Github commit 40523b9 shows one initial implementation of the APL code that takes APL arrays and namespaces and converts them into namespaces that ⎕JSON can handle and that Python knows how to interpret. This commit also shows the APL code for the reverse operation. For now, this APL code lives in the file Proxies.apln and the respective Python code lives in the file proxies.py. Everything is ready for me to hook this into the Py’n’APL machinery so that Py’n’APL uses this mechanism to pass data around…but that’s for another blog post!
Summary of Changes
GitHub’s compare feature shows all the changes I made since the commit that was the starting point for this post. The most notable changes are:
- Moving the contents of
ConversionInterface.pyandObjectWrapper.pyintoArray.py. - Adding the file
proxies.pythat will have the Python code to deal with the JSON and conversions, which will end up replacing most of the code I mentioned in the previous bullet point. - Adding the file
Proxies.aplnthat will have the APL code to deal with the JSON and conversions, which will end up replacing a chunk of code that currently lives inPy.dyalog, which is a huge file with almost all of the Py’n’APL APL code.
Blog posts in this series:


 Follow
Follow

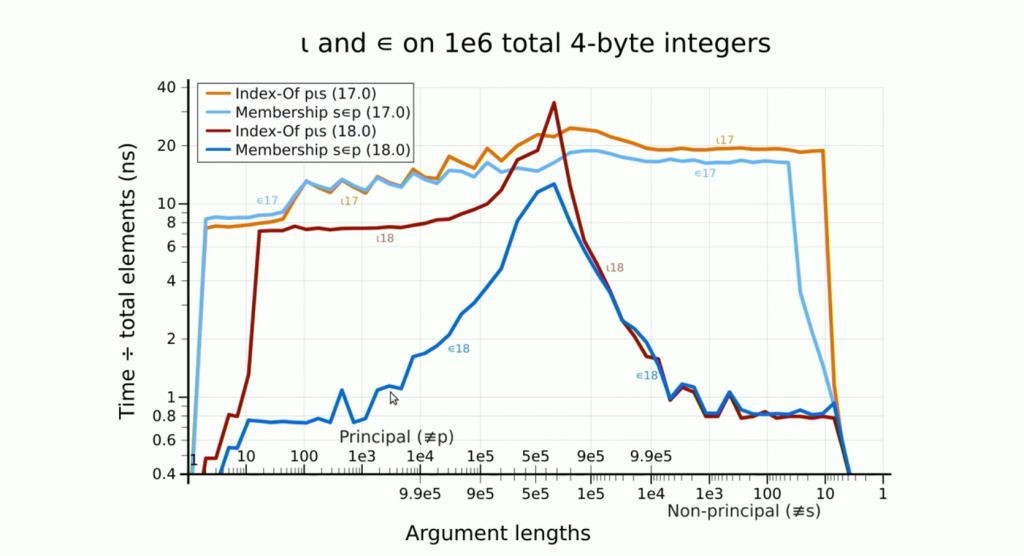
 By combining non-branching algorithms with vector instructions and a technique known as Robin Hood Hashing, Marshall is able to drive a modern CPU close to the theoretical maximum throughput, and in many cases spend less than one nanosecond searching for each item of an array.
By combining non-branching algorithms with vector instructions and a technique known as Robin Hood Hashing, Marshall is able to drive a modern CPU close to the theoretical maximum throughput, and in many cases spend less than one nanosecond searching for each item of an array.