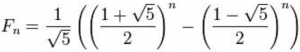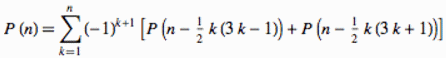Introduction

The e-mail arrived in the early afternoon from Morten, in Finland attending the FinnAPL Forest Seminar.

Background

⌺ is stencil, a new dyadic operator which will be available in version 16.0. In brief, f⌺s applies the operand function f to windows of size s. The window is moved over the argument centered over every possible position. The size is commonly odd and the movement commonly 1. For example:

   {⊂⍵}⌺5 3⊢6 5⍴⍳30
┌───────┬────────┬────────┬────────┬───────┐
│0  0  0│ 0  0  0│ 0  0  0│ 0  0  0│ 0  0 0│
│0  0  0│ 0  0  0│ 0  0  0│ 0  0  0│ 0  0 0│
│0  1  2│ 1  2  3│ 2  3  4│ 3  4  5│ 4  5 0│
│0  6  7│ 6  7  8│ 7  8  9│ 8  9 10│ 9 10 0│
│0 11 12│11 12 13│12 13 14│13 14 15│14 15 0│
├───────┼────────┼────────┼────────┼───────┤
│0  0  0│ 0  0  0│ 0  0  0│ 0  0  0│ 0  0 0│
│0  1  2│ 1  2  3│ 2  3  4│ 3  4  5│ 4  5 0│
│0  6  7│ 6  7  8│ 7  8  9│ 8  9 10│ 9 10 0│
│0 11 12│11 12 13│12 13 14│13 14 15│14 15 0│
│0 16 17│16 17 18│17 18 19│18 19 20│19 20 0│
├───────┼────────┼────────┼────────┼───────┤
│0  1  2│ 1  2  3│ 2  3  4│ 3  4  5│ 4  5 0│
│0  6  7│ 6  7  8│ 7  8  9│ 8  9 10│ 9 10 0│
│0 11 12│11 12 13│12 13 14│13 14 15│14 15 0│
│0 16 17│16 17 18│17 18 19│18 19 20│19 20 0│
│0 21 22│21 22 23│22 23 24│23 24 25│24 25 0│
├───────┼────────┼────────┼────────┼───────┤
│0  6  7│ 6  7  8│ 7  8  9│ 8  9 10│ 9 10 0│
│0 11 12│11 12 13│12 13 14│13 14 15│14 15 0│
│0 16 17│16 17 18│17 18 19│18 19 20│19 20 0│
│0 21 22│21 22 23│22 23 24│23 24 25│24 25 0│
│0 26 27│26 27 28│27 28 29│28 29 30│29 30 0│
├───────┼────────┼────────┼────────┼───────┤
│0 11 12│11 12 13│12 13 14│13 14 15│14 15 0│
│0 16 17│16 17 18│17 18 19│18 19 20│19 20 0│
│0 21 22│21 22 23│22 23 24│23 24 25│24 25 0│
│0 26 27│26 27 28│27 28 29│28 29 30│29 30 0│
│0  0  0│ 0  0  0│ 0  0  0│ 0  0  0│ 0  0 0│
├───────┼────────┼────────┼────────┼───────┤
│0 16 17│16 17 18│17 18 19│18 19 20│19 20 0│
│0 21 22│21 22 23│22 23 24│23 24 25│24 25 0│
│0 26 27│26 27 28│27 28 29│28 29 30│29 30 0│
│0  0  0│ 0  0  0│ 0  0  0│ 0  0  0│ 0  0 0│
│0  0  0│ 0  0  0│ 0  0  0│ 0  0  0│ 0  0 0│
└───────┴────────┴────────┴────────┴───────┘
   {+/,⍵}⌺5 3⊢6 5⍴⍳30
 39  63  72  81  57
 72 114 126 138  96
115 180 195 210 145
165 255 270 285 195
152 234 246 258 176
129 198 207 216 147

In addition, for matrix right arguments with movement 1, special code is provided for the following operand functions:

{∧/,⍵}   {∨/,⍵}   {=/,⍵}   {≠/,⍵} 

{⍵}      {,⍵}     {⊂⍵}     {+/,⍵}

{+/,A×⍵}     {E<+/,A×⍵}       
{+/⍪A×⍤2⊢⍵}  {E<+/⍪A×⍤2⊢⍵}

The comparison < can be one of < ≤ = ≠ ≥ >.

The variables r g b in the problem are integer matrices with shape 227 316 having values between 0 and 255. For present purposes we can initialize them to random values:

   r←¯1+?227 316⍴256
   g←¯1+?227 316⍴256
   b←¯1+?227 316⍴256

Opening Moves

I had other obligations and did not attend to the problem until 7 PM. A low-hanging fruit was immediately apparent: {+/,⍵×A}⌺s is not implemented by special code but {+/,A×⍵}⌺s is. The difference in performance is significant:

   edges1←{⍺←0.7 ⋄ 1 1↓¯1 ¯1↓⍺<(|EdgeDetect apply1 ⍵)÷1⌈(+⌿÷≢),⍵}
   apply1←{stencil←⍺ ⋄ {+/,stencil×⍵}⌺(⍴stencil)⊢⍵}

   cmpx 'e←⊃∨/0.2 edges1¨r g b' 'e←⊃∨/0.2 edges ¨r g b'
  e←⊃∨/0.2 edges1¨r g b → 8.0E¯3 |     0% ⎕
  e←⊃∨/0.2 edges ¨r g b → 6.1E¯1 | +7559% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕

I fired off an e-mail reporting this good result, then turned to other more urgent matters. An example of the good being an enemy of the better, I suppose.

When I returned to the problem at 11 PM, the smug good feelings have largely dissipated:

• Why should {+/,A×⍵}⌺s be so much faster than {+/,⍵×A}⌺s? That is, why is there special code for the former but not the latter? (Answer: all the special codes end with … ⍵}.)
• I can not win: If the factor is small, then why isn’t it larger; if it is large, it’s only because the original code wasn’t very good.
• The large factor is because, for this problem, C (special code) is still so much faster than APL (magic function).
• If the absolute value can somehow be replaced, the operand function can then be in the form {E<+/,A×⍵}⌺s, already implemented by special code. Alternatively, {E<|+/,A×⍵}⌺s can be implemented by new special code.

Regarding the last point, the performance improvement potentially can be:

   edges2←{⍺←0.7 ⋄ 1 1↓¯1 ¯1↓(⍺ EdgeDetect)apply2 ⍵}
   apply2←{threshold stencil←⍺ ⋄ 
                    {threshold<+/,stencil×⍵}⌺(⍴stencil)⊢⍵}

   cmpx (⊂'e←⊃∨/0.2 edges'),¨'21 ',¨⊂'¨r g b'
  e←⊃∨/0.2 edges2¨r g b → 4.8E¯3 |      0%
* e←⊃∨/0.2 edges1¨r g b → 7.5E¯3 |    +57%
* e←⊃∨/0.2 edges ¨r g b → 7.4E¯1 | +15489% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕

The * in the result of cmpx indicates that the expressions don’t give the same results. That is expected; edges2 is not meant to give the same results but is to get a sense of the performance difference. (Here, an additional factor of 1.57.)

edges1 has the expression ⍺<matrix÷1⌈(+⌿÷≢),⍵ where ⍺ and the divisor are both scalars. Reordering the expression eliminates one matrix operation: (⍺×1⌈(+⌿÷≢),⍵)<matrix. Thus:

   edges1a←{⍺←0.7 ⋄ 1 1↓¯1 ¯1↓(⍺×1⌈(+⌿÷≢),⍵)<|EdgeDetect apply1 ⍵}

   cmpx (⊂'e←⊃∨/0.2 edges'),¨('1a' '1 ' '  '),¨⊂'¨r g b'
  e←⊃∨/0.2 edges1a¨r g b → 6.3E¯3 |      0%
  e←⊃∨/0.2 edges1 ¨r g b → 7.6E¯3 |    +22%
  e←⊃∨/0.2 edges  ¨r g b → 6.5E¯1 | +10232% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕

The time was almost 1 AM. To bed.

Further Maneuvers

Fresh and promising ideas came with the morning. The following discussion applies to the operand function {+/,A×⍵}.

(0) Scalar multiple: If all the elements of A are equal, then {+/,A×⍵}⌺(⍴A)⊢r ←→ (⊃A)×{+/,⍵}⌺(⍴A)⊢r.

   A←3 3⍴?17
   ({+/,A×⍵}⌺(⍴A)⊢r) ≡ (⊃A)×{+/,⍵}⌺(⍴A)⊢r
1

(1) Sum v inner product: {+/,⍵}⌺(⍴A)⊢r is significantly faster than {+/,A×⍵}⌺(⍴A)⊢r because the former exploits mathematical properties absent from the latter.

   A←?3 3⍴17
   cmpx '{+/,⍵}⌺(⍴A)⊢r' '{+/,A×⍵}⌺(⍴A)⊢r'
  {+/,⍵}⌺(⍴A)⊢r   → 1.4E¯4 |    0% ⎕⎕⎕
* {+/,A×⍵}⌺(⍴A)⊢r → 1.3E¯3 | +828% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕

(The * in the result of cmpx is expected.)

(2) Linearity: the stencil of the sum equals the sum of the stencils.

   A←?3 3⍴17
   B←?3 3⍴17
   ({+/,(A+B)×⍵}⌺(⍴A)⊢r) ≡ ({+/,A×⍵}⌺(⍴A)⊢r) + {+/,B×⍵}⌺(⍴A)⊢r 
1

(3) Middle: If B is zero everywhere except the middle, then {+/,B×⍵}⌺(⍴B)⊢r ←→ mid×r where mid is the middle value.

   B←(⍴A)⍴0 0 0 0 9
   B
0 0 0
0 9 0
0 0 0
   ({+/,B×⍵}⌺(⍴B)⊢r) ≡ 9×r
1

(4) A faster solution.

   A←EdgeDetect
   B←(⍴A)⍴0 0 0 0 9
   C←(⍴A)⍴¯1
   A B C
┌────────┬─────┬────────┐
│¯1 ¯1 ¯1│0 0 0│¯1 ¯1 ¯1│
│¯1  8 ¯1│0 9 0│¯1 ¯1 ¯1│
│¯1 ¯1 ¯1│0 0 0│¯1 ¯1 ¯1│
└────────┴─────┴────────┘
   A ≡ B+C
1

Whence:

   ({+/,A×⍵}⌺(⍴A)⊢r) ≡ ({+/,B×⍵}⌺(⍴A)⊢r) + {+/,C×⍵}⌺(⍴A)⊢r ⍝ (2)
1
   ({+/,A×⍵}⌺(⍴A)⊢r) ≡ ({+/,B×⍵}⌺(⍴A)⊢r) - {+/,⍵}⌺(⍴A)⊢r   ⍝ (0)
1
   ({+/,A×⍵}⌺(⍴A)⊢r) ≡ (9×r) - {+/,⍵}⌺(⍴A)⊢r                ⍝ (3)
1

Putting it all together:

edges3←{
  ⍺←0.7
  mid←⊃EdgeDetect↓⍨⌊2÷⍨⍴EdgeDetect
  1 1↓¯1 ¯1↓(⍺×1⌈(+⌿÷≢),⍵)<|(⍵×1+mid)-{+/,⍵}⌺(⍴EdgeDetect)⊢⍵
}

Comparing the various edges:

   x←(⊂'e←⊃∨/0.2 edges'),¨('3 ' '2 ' '1a' '1 ' '  '),¨⊂'¨r g b'
   cmpx x
  e←⊃∨/0.2 edges3 ¨r g b → 3.4E¯3 |      0%
* e←⊃∨/0.2 edges2 ¨r g b → 4.3E¯3 |    +25%
  e←⊃∨/0.2 edges1a¨r g b → 6.4E¯3 |    +88%
  e←⊃∨/0.2 edges1 ¨r g b → 7.5E¯3 |   +122%
  e←⊃∨/0.2 edges  ¨r g b → 6.5E¯1 | +19022% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕

Fin

I don’t know if the Finns would be impressed. The exercise has been amusing in any case.

Follow

(⎕io←0 and timings are done in Dyalog version 15.0.)

Table Look-Up

Some functions can be computed faster by table look-up than a more traditional and more conventional calculation. For example:

      b←?1e6⍴2

      cmpx '*b' '(*0 1)[b]'
 *b        → 1.32E¯2 |   0% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕
 (*0 1)[b] → 1.23E¯3 | -91% ⎕⎕⎕

Some observations about this benchmark:

(a) The advantage of table look-up depends on the time to calculate the function directly, versus the time to do indexing, ⍺[⍵] or ⍵⌷⍺, plus a small amount of time to calculate the function on a (much) smaller representative set.

Indexing is particularly efficient when the indices are boolean:

      bb←b,1
      bi←b,2
      cmpx '2 3[bb]' '2 3 3[bi]'
 2 3[bb]   → 1.12E¯4 |    0% ⎕⎕⎕⎕⎕
 2 3 3[bi] → 7.39E¯4 | +558% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕

bi is the same as bb except that the last element of 2 forces it to be 1-byte integers (for bi) instead of 1-bit booleans (for bb).

(b) Although the faster expression works best with 0-origin, the timing for 1-origin is similar.

      cmpx '*b' '{⎕io←0 ⋄ (*0 1)[⍵]}b'
 *b                   → 1.32E¯2 |   0% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕
 {⎕io←0 ⋄ (*0 1)[⍵]}b → 1.22E¯3 | -91% ⎕⎕⎕

That is, if the current value of ⎕io is 1, the implementation can use a local ⎕io setting of 0.

(c) The fact that *b is currently slower than (*0 1)[b] represents a judgment by the implementers that *b is not a sufficiently common computation to warrant writing faster code for it. Other similar functions already embody the table look-up technique:

      cmpx '⍕b' '¯1↓,(2 2⍴''0 1 '')[b;]'
 ⍕b                   → 6.95E¯4 |  0% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕
 ¯1↓,(2 2⍴'0 1 ')[b;] → 6.92E¯4 | -1% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕

Small Domains

Table look-up works best for booleans, but it also works for other small domains such as 1-byte integers:

      i1←?1e6⍴128    ⍝ 1-byte integers

      cmpx '*i1' '(*⍳128)[i1]'
 *i1         → 1.48E¯2 |   0% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕
 (*⍳128)[i1] → 9.30E¯4 | -94% ⎕⎕

      cmpx '○i1' '(○⍳128)[i1]'
 ○i1         → 2.78E¯3 |   0% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕
 (○⍳128)[i1] → 9.25E¯4 | -67% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕

In general, a table for 1-byte integers needs to have values for ¯128+⍳256. Here ⍳128 is used to simulate that in C indexing can be done on 1-byte indices without extra computation on the indices. In APL, general 1-byte indices are used as table[i1+128]; in C, the expression is (table+offset)[i].

Domains considered “small” get bigger all the time as machines come equipped with ever larger memories.

Larger Domains

Table look-up is applicable when the argument is not a substantial subset of a large domain and there is a fast way to detect that it is not.

      i4s←1e7+?1e6⍴1e5    ⍝ small-range 4-byte integers

      G←{(⊂u⍳⍵)⌷⍺⍺ u←∪⍵}

      cmpx '⍟i4s' '⍟G i4s'
 ⍟i4s   → 1.44E¯2 |   0% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕
 ⍟G i4s → 9.59E¯3 | -34% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕

The definition of G implements that the argument is not used directly as indices (as in (⊂⍵)⌷⍺⍺ u) but needed to be looked up, the u⍳⍵ in (⊂u⍳⍵)⌷⍺⍺ u. Thus both index-of and indexing are key enablers for making table look-up competitive.

§4.3 of Notation as a Tool of Thought presents a different way to distribute the results of a calculation on the “nub” (unique items). But it takes more time and space and is limited to numeric scalar results.

      H←{(⍺⍺ u)+.×(u←∪⍵)∘.=⍵}

      i4a←1e7+?1e4⍴1e3    ⍝ small-range 4-byte integers

      cmpx '⍟i4a' '⍟G i4a' '⍟H i4a'
 ⍟i4a   → 1.56E¯4 |       0%
 ⍟G i4a → 6.25E¯5 |     -60%
 ⍟H i4a → 1.78E¯1 | +113500% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕

The benchmark is done on the smaller i4a as a benchmark on i4s founders on the ≢∪⍵ by ≢⍵ boolean matrix (for i4s, 12.5 GB = ×/ 0.125 1e5 1e6) created by H.

Mathematical Background

“New Math” teaches that a function is a set of ordered pairs whose first items are unique:

*⍵: {(⍵,*⍵)|⍵∊C}      The set of all (⍵,*⍵) where ⍵ is a complex number
⍟⍵: {(⍵,⍟⍵)|⍵∊C~{0}}  The set of all (⍵,⍟⍵) where ⍵ is a non-zero complex number
○⍵: {(⍵,○⍵)|⍵∊C}      The set of all (⍵,○⍵) where ⍵ is a complex number
⍕⍵: {(⍵,⍕⍵)|0=⍴⍴⍵}    The set of all (⍵,⍕⍵) where ⍵ is a scalar

When ⍵ is restricted (for example) to the boolean domain, the functions, the sets of ordered pairs, are more simply represented by enumerating all the possibilities:

*⍵: {(0,1), (1,2.71828)}
⍟⍵: {(0,Err), (1,0)}
○⍵: {(0,0), (1,3.14159)}
⍕⍵: {(0,'0'), (1,'1')}

Realized and Potential Performance Improvements

realized (available no later than 15.0)

potential (non-exhaustive list)

a is a scalar; f and g are primitive scalar dyadic functions.

Follow

Abstract

Some functions are simply stated and easily understood as multiply-recursive functions. For example, the Fibonacci numbers are {1≥⍵:⍵ ⋄ (∇ ⍵-2)+∇ ⍵-1}. A drawback of multiple recursion is abysmal performance even for moderate-sized arguments, consequently motivating resorts to circumlocutions. The memo operator addresses the performance problem and restores multiple recursion to the toolkit of thought. We present a memo operator modelled as a 6-line d-operator.

⎕io←0 throughout.

The Man Who Knew Infinity

Jay sent out an e-mail asking who would be interested to go see the film The Man Who Knew Infinity. Fiona’s response: “Ah, Mr. 1729; I’m in.” John was game, and so was I.

The Number of Partitions
Nick found an essay by Stephen Wolfram on Ramanujan written on occasion of the film, wherein Wolfram said:

In[1]:= PartitionsP[200]
Out[1]= 3 972 999 029 388

A partition of a non-negative integer n is a vector v of positive integers such that n = +/v, where the order in v is not significant. For example, the partitions of the first seven non-negative integers are:

┌┐
││
└┘
┌─┐
│1│
└─┘
┌─┬───┐
│2│1 1│
└─┴───┘
┌─┬───┬─────┐
│3│2 1│1 1 1│
└─┴───┴─────┘
┌─┬───┬───┬─────┬───────┐
│4│3 1│2 2│2 1 1│1 1 1 1│
└─┴───┴───┴─────┴───────┘
┌─┬───┬───┬─────┬─────┬───────┬─────────┐
│5│4 1│3 2│3 1 1│2 2 1│2 1 1 1│1 1 1 1 1│
└─┴───┴───┴─────┴─────┴───────┴─────────┘
┌─┬───┬───┬─────┬───┬─────┬───────┬─────┬───────┬─────────┬───────────┐
│6│5 1│4 2│4 1 1│3 3│3 2 1│3 1 1 1│2 2 2│2 2 1 1│2 1 1 1 1│1 1 1 1 1 1│
└─┴───┴───┴─────┴───┴─────┴───────┴─────┴───────┴─────────┴───────────┘

Can we compute the partition counting function “instantaneously” in APL?

We will use a recurrence relation derived from the pentagonal number theorem, proved by Euler more than 160 years before Hardy and Ramanujan:

equation (11) in http://mathworld.wolfram.com/PartitionFunctionP.html. In APL:

      pn  ← {0≥⍵:0=⍵ ⋄ -/+⌿∇¨rec ⍵}
      rec ← {⍵ - (÷∘2 (×⍤1) ¯1 1 ∘.+ 3∘×) 1+⍳⌈0.5*⍨⍵×2÷3}

      pn¨0 1 2 3 4 5 6
1 1 2 3 5 7 11

      pn 30
5604

Warning: don’t try pn 200 because that would take a while! Why? pn 200 would engender pn being applied to each element of rec 200 and:

   rec 200
199 195 188 178 165 149 130 108 83 55 24 ¯10
198 193 185 174 160 143 123 100 74 45 13 ¯22

Each of the non-negative values would itself engender further recursive applications.

A Memo Operator

I recalled from J the memo adverb (monadic operator) M. Paraphrasing the J dictionary: f M is the same as f but may keep a record of the arguments and results for reuse. It is commonly used for multiply-recursive functions. Sounds like just the ticket!

The functionistas had previously implemented a (dyadic) memo operator. The version here is more restrictive but simpler. The restrictions are as follows:

• The cache is constructed “on the fly” and is discarded once the operand finishes execution.
• The operand is a dfn {condition:basis ⋄ expression} where none of condition, base and expression contain a ⋄ and recursion is denoted by ∇ in expression
• The arguments are scalar integers.
• The operand function does not have ¯1 as a result.
• A recursive call is on a smaller integer.

With these restrictions, our memo operator can be defined as follows:

M←{
 f←⍺⍺
 i←2+'⋄'⍳⍨t←3↓,⎕CR'f'
 0=⎕NC'⍺':⍎' {T←(1+  ⍵)⍴¯1 ⋄  {',(i↑t),'¯1≢T[⍵]  :⊃T[⍵]   ⋄ ⊃T[⍵]  ←⊂',(i↓t),'⍵}⍵'
          ⍎'⍺{T←(1+⍺,⍵)⍴¯1 ⋄ ⍺{',(i↑t),'¯1≢T[⍺;⍵]:⊃T[⍺;⍵] ⋄ ⊃T[⍺;⍵]←⊂',(i↓t),'⍵}⍵'
}

      pn M 10
42

      pn 10
42

Obviously, the ⍎ lines in M are crucial. When the operand is pn, the expression which is executed is as follows; the characters inserted by M are shown in red.

{T←(1+⍵)⍴¯1 ⋄ {0≥⍵:0=⍵ ⋄ ¯1≢T[⍵]:⊃T[⍵] ⋄ ⊃T[⍵]←⊂-/+⌿∇¨rec ⍵}⍵}⍵

The machinations produce a worthwhile performance improvement:

      pn M 30
5604
      cmpx 'pn M 30'
3.94E¯4
      cmpx 'pn 30'
4.49E1 
      4.49e1 ÷ 3.94e¯4
113959

That is, pn M 30 is faster than pn 30 by a factor of 114 thousand.

Can APL compute pn M 200 “instantaneously”? Yes it can, for a suitable definition of “instantaneous”.

      cmpx 'm←pn M 200'
4.47E¯3
      m
3.973E12
      0⍕m
 3972999029388

M also works on operands which are anonymous, dyadic, or have non-scalar results.

Fibonacci Numbers

   fib←{1≥⍵:⍵ ⋄ (∇ ⍵-2)+∇ ⍵-1}

   fib¨ ⍳15
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377
   fib M¨ ⍳15
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377

   cmpx 'fib 30'
1.45E0 
   cmpx 'fib M 30'
1.08E¯4

Anonymous function:

      {1≥⍵:⍵ ⋄ (∇ ⍵-2)+∇ ⍵-1}M¨ ⍳15
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377

Combinations
⍺ comb ⍵ produces a matrix of all the size-⍺ combinations of ⍳⍵. The algorithm is from the venerable APL: An Interactive Approach by Gilman and Rose.

      comb←{(⍺≥⍵)∨0=⍺:((⍺≤⍵),⍺)⍴⍳⍺ ⋄ (0,1+(⍺-1)∇ ⍵-1)⍪1+⍺ ∇ ⍵-1}

      3 comb 5
0 1 2
0 1 3
0 1 4
0 2 3
0 2 4
0 3 4
1 2 3
1 2 4
1 3 4
2 3 4

      3 (comb ≡ comb M) 5
1

      cmpx '8 comb M 16' '8 comb 16'
  8 comb M 16 → 1.00E¯3 |     0% ⎕                             
  8 comb 16   → 3.63E¯2 | +3526% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕

A faster comb is possible without a memo operator, but it’s not easy. (See for example section 4.1 of my APL87 paper.) A memo operator addresses the performance problem with multiple recursion and restores it to the toolkit of thought.

Presented at the BAA seminar at the Royal Society of Arts on 2016-05-20

Follow